Regulatory PID są najczęściej stosowane do wpływania na określone zmienne mierzone. Jako sprytne regulatory 3 w 1 sprawdzają się na co dzień w wielu systemach przemysłowych i sterują bardzo dokładnie zgodnie z wartością zadaną. Tutaj znajdziesz najważniejsze fakty i liczby dotyczące regulacji PID.
Cyfrowy regulator PID może być wszechstronnie programowany i parametryzowany przez zintegrowany mikroprocesor. Działa on na zasadzie proporcjonalności, całkowania i różniczkowania (PID), dzięki czemu intensywność działania poszczególnych elementów jest dostosowywana do sterowanego systemu. Odbywa się to poprzez wymiarowanie parametrów regulacyjnych:
Zasada działania regulatora PID jest stosunkowo prosta do wyjaśnienia. Bez względu na to, czy jest to regulator PID temperatury, czy regulator PID wilgotności, sterownik zawsze stara się dostosować określoną zmienną regulowaną do wartości zadanej na podstawie wartości rzeczywistej. W tym celu regulator P wzmacnia odchylenie regulacji, regulator I zwiększa poziom wyjściowy w przypadku istniejącego odchylenia regulacji, a regulator D przeciwdziała zmianom wartości rzeczywistej. Jeśli nie wszystkie elementy są potrzebne do sterowania, można je dezaktywować. W zależności od zastosowania są one wtedy określane jako regulator PI, regulator P, regulator PD lub regulator I.
W większości zastosowań struktura PID charakteryzuje się najlepszym zachowaniem regulacyjnym. Kompaktowe regulatory PID oraz sterowniki działające w oparciu o algorytm regulacji PID są bardzo rozpowszechnione w dziedzinie regulacji temperatury, umożliwiają także bezpośrednie podłączenie termometrów oporowych i termopar. Niektóre kontrolowane zmienne wymagają wyłączenia pewnych elementów, w tym między innymi prędkości i przepływu.
Człon P (proporcjonalny) reaguje bardzo szybko i wzmacnia różnicę regulacyjną; jego stałe odchylenie regulacyjne ma negatywny wpływ. Odpowiedzialnym parametrem sterującym jest pasmo proporcjonalności Xp. Przy mniejszych wymiarach Xp regulator działa szybciej, a odchylenie regulacji jest mniejsze. Jednak cały system ma tendencję do coraz większych oscylacji.
Człon I (całkujący) eliminuje odchylenie regulacji. Jeśli czas zerowania Tn jest ustawiony na mniejszą wartość, regulator szybciej buduje swój poziom wyjściowy i szybciej przeciwdziała odchyleniom regulacyjnym. Jeśli jednak nastaw regulatora PID będzie zbyt mały, wystąpią również zachowania oscylacyjne.
Człon D (różniczkujący) przeciwdziała zmianom wartości rzeczywistej. W przypadku regulatora ogrzewania oznacza to, że proporcja jest zmniejszana, gdy wartość rzeczywista wzrasta, i zwiększana, gdy wartość rzeczywista maleje. Opisane zachowanie ma charakter tłumiący. Odpowiedzialnym parametrem jest czas pochodnej Tv. Im większy jest ustawiony czas Tv, tym większy jest opisany efekt.
Zachowanie układów regulowanych zawsze zależy od punktu pracy. Dlatego przed optymalizacją należy doprowadzić instalację do takiego stanu pracy, dla którego później oczekuje się korzystnych parametrów regulacyjnych. Na przykład przed optymalizacją piec jest obciążany, a dla przepływowego podgrzewacza wody musi być wygenerowana akceptacja. Jeśli wartość zadana musi być określona podczas optymalizacji, będzie ona znajdować się w późniejszym zakresie roboczym.
Jeśli istnieją porównywalne instalacje/pętle regulacyjne, można na próbę zastosować stosowane tam parametry regulacyjne. Jeśli takie podejście nie prowadzi do celu, można zastosować jedną z poniższych metod optymalizacji.
Metoda wibracyjna według Zieglera i Nicholsa
Metoda ta jest stosowana w przypadku stosunkowo szybko sterowanych systemów. W celu przygotowania parametryzuje się strukturę P i ustawia stosunkowo dużą wartość XP. Wartość zadana w późniejszym zakresie roboczym jest zdefiniowana na poniższym rysunku.
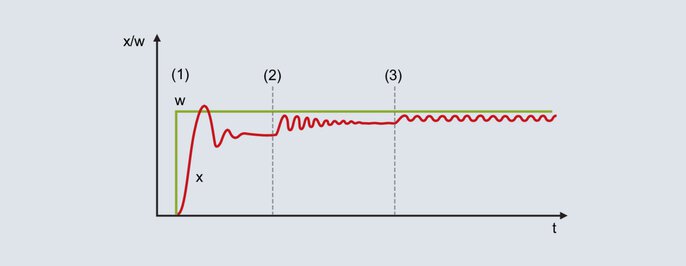
Rys. 52: Krzywa wartości zadanej i rzeczywistej przy zastosowaniu metody oscylacyjnej
Przy ustawieniu stosunkowo dużego pasma proporcjonalnego wartość rzeczywista dąży do wartości końcowej z niewielką tendencją do oscylacji [rys. 52 (1)]. Ze względu na nieistniejącą strukturę I występuje stałe odchylenie regulacji.
Wartość XP zostaje zredukowana (Rysunek 52 [2]): Wartość rzeczywista wzrasta i biegnie do wartości końcowej z większą tendencją do oscylacji. Pasmo proporcjonalne może być zmniejszane kilkakrotnie, aż wartość rzeczywista będzie trwale oscylować (rysunek 52 [3]). Pasmo proporcjonalne wymagane do takiego zachowania nazywa się XPk (krytyczne Xp) i musi być określone możliwie dokładnie (nie zmniejszać Xp w zbyt dużych krokach).
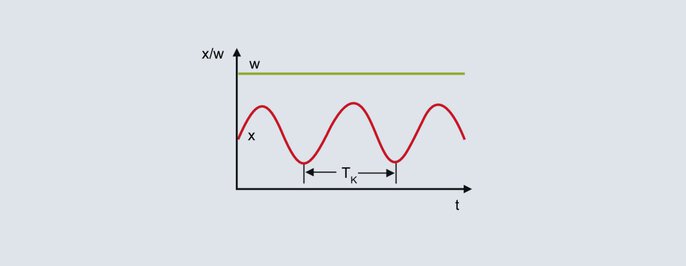
Okres krytyczny
Na podstawie ciągłych oscylacji wartości rzeczywistej na górnym rysunku, okres krytyczny TK jest wykorzystywany do wyznaczenia drugiego parametru procesu. Okres krytyczny TK (w sekundach) wynika na przykład z przedziału czasu pomiędzy dwoma wartościami minimalnymi. XPk i TK są wstawiane do poniższej tabeli dla żądanej struktury regulatora:
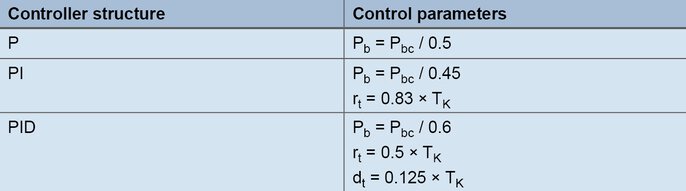
Wzory na ustawienia według metody oscylacyjnej
Procedura zgodna z odpowiedzią z krokiem odległości wg Chien, Hrones i Reswic
Dzięki tej metodzie parametry sterowania są wyznaczane w sposób stosunkowo oszczędny czasowo, nawet w przypadku powolnych układów regulowanych. Metoda ta jest stosowana dla układów regulowanych drugiego rzędu i wyższych, a jej szczególną cechą jest możliwość rozróżnienia formuł dla polecenia i odpowiedzi na zakłócenie. W przypadku wzorów regułowych współczynnik przenoszenia układu regulowanego, czas opóźnienia i czas kompensacji są wyznaczane na podstawie odpowiedzi skokowej.
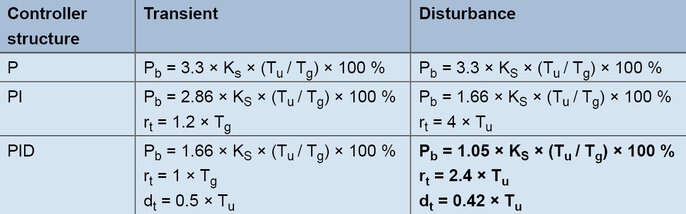
Wzory do tworzenia według reakcji stopnia linii
W piecu laboratoryjnym ma być zastosowany regulator cyfrowy o strukturze PID. Celem jest uzyskanie dobrego zachowania w warunkach zakłóceń, typowe wartości zadane wynoszą 200 °C. W trybie ręcznym poziom wyjściowy jest zwiększany stopniowo, aż wartość rzeczywista będzie nieco niższa od późniejszej wartości zadanej (w każdym przypadku należy poczekać na procesy kompensacji). Na przykład temperatura 180 °C jest osiągana przy poziomie wyjściowym 60 %. Począwszy od 60 %, poziom wyjściowy jest stopniowo zwiększany do 80 %, a wartość rzeczywista jest rejestrowana.
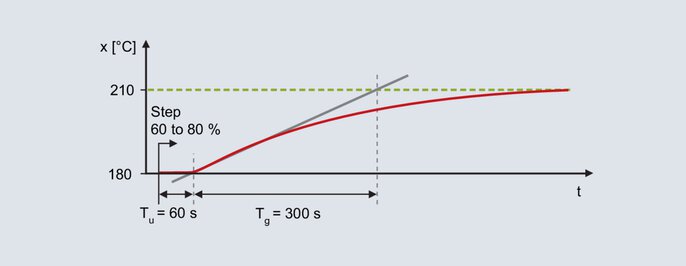
Odpowiedź skokowa pieca laboratoryjnego
Odpowiedź skokowa jest wyznaczana za pomocą tangensa skrętu: czas opóźnienia Tu = 60 s, czas kompensacji Tg = 300 s. Współczynnik przenoszenia układu sterowanego wynika ze zmiany wartości rzeczywistej podzielonej przez krok wyjściowy.
Równanie 22
Korzystając z powyższych zasad, można wyznaczyć następujące parametry zachowania w warunkach zakłóceń:
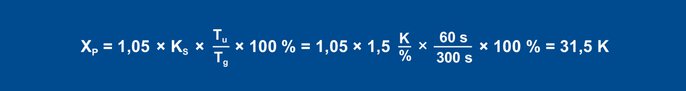
Równanie 23
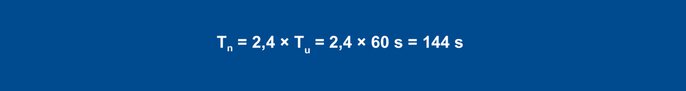
Równanie 24
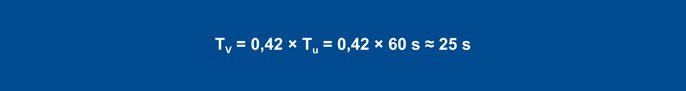
Równanie 25
Krok wyjściowy musi być wykonywany w zakresie kolejnego punktu pracy. Wysokość kroku musi być jednak na tyle duża, aby można było ocenić krzywą wartości procesowej. Po określeniu kroku wyjściowego oczekuje się na wartość końcową wartości rzeczywistej; alternatywą oszczędzającą czas jest procedura według szybkości narastania.
Procedura w zależności od tempa wzrostu
Jeśli chodzi o reakcję na zmianę kroku, procedura jest taka sama jak w przypadku reakcji na zmianę odległości. Przed zmianą kroku określany jest poziom wyjściowy, przy którym wartość rzeczywista jest nieco niższa od wartości zadanej używanej później.
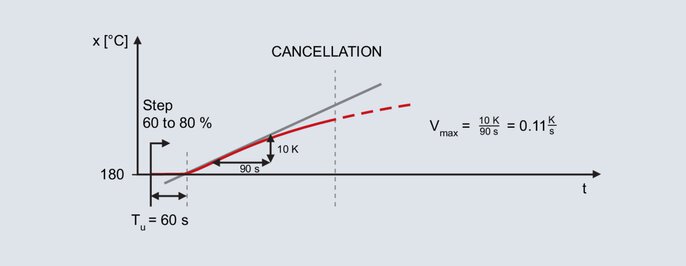
Krzywa wartości rzeczywistej dla metody w zależności od prędkości przesuwu
Ponownie ustawia się stopień dla wspomnianego już pieca laboratoryjnego; kolejny punkt pracy również wynosi 200 °C. Określając stopień działania 60 % w trybie ręcznym, uzyskuje się rzeczywistą wartość 180 °C. Stopień wyjściowy jest zwiększany stopniowo do 80 %.
Po ustawieniu stopnia wartość rzeczywista wzrasta po pewnym czasie. Rejestrowanie jest kontynuowane do momentu, gdy wartość rzeczywista osiągnie maksymalne nachylenie. Również w tej metodzie rysowana jest styczna skręcająca i określany jest czas opóźnienia. Drugim parametrem jest maksymalna szybkość narastania, która odpowiada nachyleniu stycznej skręcającej. Maksymalną szybkość wznoszenia określa się za pomocą trójkąta nachylenia na stycznej do zakrętu:
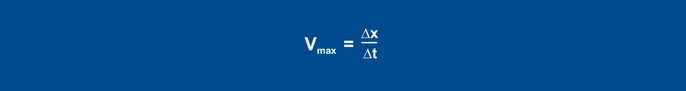
Równanie 26
Wyznaczone wartości Vmax (0,11 K/s) i Tu (60 s) wstawiono do następujących wzorów:
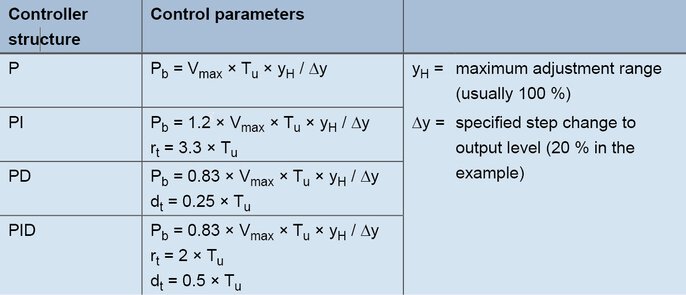
Wzory na ustawienie w zależności od szybkości narastania
W przypadku regulatora PID wartości te uzyskuje się za pomocą następujących wzorów:
Równanie 27
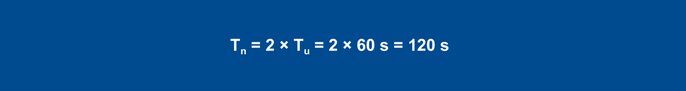
Równanie 28
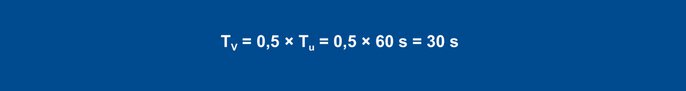
Równanie 29
Empiryczna metoda wyznaczania parametrów sterowania
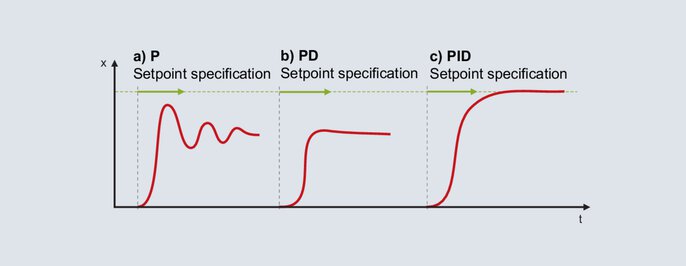
W tej metodzie korzystne nastawy dla elementów P, D i I są określane jedna po drugiej. Począwszy od stanu początkowego (poziom wyjściowy 0%), zawsze określana jest typowa wartość zadana; dlatego metoda ta może być stosowana tylko w przypadku stosunkowo szybko regulowanych układów (np. układów z szybką regulacją temperatury i zmiennymi regulowanymi, takimi jak prędkość lub natężenie przepływu).
Nastawy regulatora PID według metody empirycznej
W przypadku regulatora cyfrowego aktywowana jest struktura P. Pasmo proporcjonalne jest ustawione na stosunkowo dużą wartość (wymiarowanie zależy od sterowanego systemu), a wartość zadana jest określona w późniejszym zakresie roboczym. Wartość rzeczywista będzie powoli zbliżać się do wartości końcowej, co spowoduje stosunkowo duże odchylenie regulacji. Następnie wartość zadana jest określana za pomocą coraz mniejszego pasma proporcjonalności XP. Celem jest taka wartość Xp, przy której wartość rzeczywista osiąga stabilną wartość końcową po dwóch do trzech pełnych oscylacjach (rys. 56a). W przypadku rozruchu tłumionego struktura jest zmieniana z P na PD. Zaczynając od małej nastawy czasu pochodnej, wartość zadana jest określana z coraz większą wartością Tv. Jeśli wartość procesu osiąga wartość końcową z najmniejszą możliwą oscylacją, mamy do czynienia z korzystnym Tv (rys. 56b).
Uwaga: Gdy tylko regulator choć raz podczas rozruchu ustawi poziom wyjściowy na 0%, Tv jest ustawiona zbyt wysoko.
Po przejściu na strukturę PID aktywowana jest składowa I. Czas zerowania Tn jest zwykle ustawiany korzystnie, z czterokrotną wartością poprzednio ustalonego Tv. Rysunek 56c pokazuje zachowanie dla nastawy Tn = 4 × Tv.
W przypadku niektórych linii nie wszystkie elementy mogą zostać aktywowane. Jeśli konstrukcja P powoduje niestabilne zachowanie już przy dużych ustawieniach XP, nie można zastosować ani konstrukcji P, ani D. Stosuje się regulator I. Używany jest regulator I.
Jeśli optymalizacja regulatora P zakończyła się sukcesem, ale wprowadzenie składowej D powoduje niestabilność pętli sterowania, stosuje się strukturę PI.
Zastosowanie przedstawionych metod optymalizacji najprawdopodobniej spowoduje uzyskanie stabilnego, ale nie optymalnego zachowania regulatora. Ręczne dostrojenie pozwoli jeszcze bardziej poprawić wynik regulacji. Jeśli zachowanie regulatora PID można przypisać do jednej z krzywych od 62b do 62e, poniżej znajdują się instrukcje dotyczące dalszej optymalizacji.
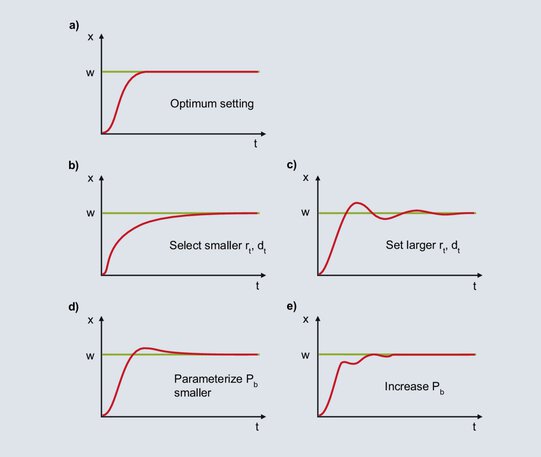
Rys. 62: Uwagi dotyczące dostrajania regulatora PID.
a)
Na wykresie przedstawiono optymalne zachowanie regulatora PID.
b)
Po określeniu wartości zadanej, wartość procesu rośnie gwałtownie aż do osiągnięcia pasma proporcjonalności. Gdy wartość procesu osiągnie pasmo proporcjonalności, składowa P zostaje zredukowana, a składowa I zapewnia osiągnięcie wartości zadanej. Ze względu na stosunkowo duże nastawy Tn, wzrost składowej I jest powolny i odchylenie regulacji jest powoli eliminowane. Aby uzyskać szybsze całkowanie, należy ustawić mniejszą wartość Tn; Tv jest również zmniejszana zgodnie ze stosunkiem Tv/Tn = 1/4.
c)
Gdy wartość procesu wejdzie w pasmo proporcjonalne, składowa I zwiększa współczynnik wyjściowy. Wzrost ten trwa do momentu, gdy wartość procesu osiągnie wartość zadaną. W przedstawionym przypadku składowa I zwiększa zbyt dużo mocy wyjściowej, aż do momentu, gdy uchyb regulacji zostanie wyeliminowany, a wartość procesu przekroczy wartość zadaną. Przy obecności ujemnej odchyłki systemowej poziom wyjściowy jest redukowany zbyt szybko, wartość rzeczywista spada poniżej wartości zadanej itd. Symetryczna oscylacja wartości rzeczywistej wokół wartości zadanej wskazuje, że Tn jest ustawiony na zbyt niskim poziomie. Tn należy zwiększyć, a Tv również zwiększyć zgodnie ze stosunkiem Tv / Tn = 1/4.
d)
Składowa I powstaje od momentu wejścia wartości procesowej w pasmo proporcjonalne do momentu wyeliminowania odchyłki regulacji. Ze względu na duże nastawy Xp, składowa I zaczyna tworzyć współczynnik wyjściowy już przy dużej odchyłce regulacji. Ze względu na duże odchylenie sterowania na początku, składnik I tworzy swój współczynnik wyjściowy stosunkowo szybko. Po wyeliminowaniu odchylenia regulacji składowa I jest zbyt duża, a wartość rzeczywista przekracza wartość zadaną. Przy mniejszym ustawieniu Xp składowa I zaczyna budować swój poziom wyjściowy odpowiednio wolniej, tylko przy mniejszych odchyleniach regulacyjnych. Prawdopodobieństwo wystąpienia jednorazowego przekroczenia staje się mniejsze.
e)
Jeśli XP jest ustawiony zbyt nisko, poziom wyjściowy składnika P jest redukowany na krótko przed osiągnięciem wartości zadanej. Gdy wartość procesu wejdzie w pasmo proporcjonalności, składowa P zostaje bardzo mocno zredukowana, a wartość procesu spada. Ze względu na większe odchylenie regulacji współczynnik wyjściowy wzrasta, a wartość rzeczywista rośnie. W paśmie proporcjonalnym małe zmiany wartości rzeczywistej prowadzą do dużych zmian współczynnika wyjściowego, co powoduje dużą skłonność do oscylacji. Uspokojenie osiąga się przez zwiększenie pasma proporcjonalności.
